Die Koordinaten p_x und p_y sind Elemente aus den reellen Zahlen. Die Punkte auf einem Bildschirm hingegen sind nur ganzzahlig. Das heißt, wenn ein Punkt P = (1.3,2.8) vorgegeben wird, muss dieser auf die Koordinaten gerundet werden, die den Punkt am besten repräsentieren. In unserem Fall wäre das der Punkt P = (1,3).

Eine Linie besteht aus einem Anfangspunkt P₁ = (x₁,y₁) und einem Endpunkt P₂ = (x₂,y₂). Gesucht sei nun der Vektor u, der von P₁ nach P₂ führt. Dabei gilt:

(10.4)

(10.5)

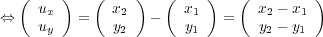(10.6)

Für die gesamte Gerade ergibt sich, in der Punkt-Richtungsform mit P₁ und dem Richtungsvektor u:

(10.7)

Da wir aber nur die Linie l und nicht die gesamte Gerade g darstellen möchten, muss r auf das Intervall [0,1] beschränkt werden. Es folgt:

(10.8)

Jetzt muss nur noch festgelegt werden, wie viele Pixel auf der Linie l ›angeschaltet‹ werden sollen, das heißt in wie vielen Schritten das Intervall [0,1] durchlaufen werden soll. Benutzt man eine feste Anzahl an Schritten, hat man ein Problem: Bei kurzen Linien würde eine feste Anzahl an Schritten dazu führen, dass einige Pixel aufgrund der Rundungen mehrfach gesetzt werden. Andersherum würden bei sehr langen Linien eventuell Lücken entstehen. Folglich erscheint es sinnvoll, die Anzahl der Schritte in Abhängig von der Länge der Linie l zu wählen. Die Länge d der Linie l berechnet sich nach Pythagoras wie folgt:

(10.9)

Mit den obigen Formeln lässt sich eine Linie einfach darstellen. In Wirklichkeit wird dies aber mit anderen Verfahren gemacht. Denn es erscheint unnötig, für jeden Punkt die x- und y-Koordinaten einzeln auszurechnen, da man die Pixel der Reihe nach setzten will. Dazu benutzt man die Geradengleichung als Funktion. Hier kann es allerdings bei sehr steilen Linien dazu kommen, dass die Pixel nicht mehr benachbart sind. Das heißt, die gezeichnete Linie weicht von der Ideallinie ab und es entstehen Lücken.

Jack Bresenham hat 1965 den nach ihm benannten Bresenham-Algorithmus⁶