|
Eigentlich gehört in diesen Bereich auch noch das weite Feld »bewegte Grafik:
Film/Video – Animation«, handelt es sich doch vereinfacht dargestellt bei einem
Film bzw. Video um bewegte Pixelgrafik und bei einer Animation um bewegte
Vektorgrafik. Aufgrund der eigenständigen Bedeutung der »bewegten Grafik«
wird sie aber in Kapitel 11 gesondert dargestellt. In Abschnitt 10.2 wird nun
detaillierter auf die Vektorgrafik und in Abschnitt 10.3 näher auf die Pixelgrafik
eingegangen.
10.2. Vektorgrafik
Ein zwei- oder dreidimensionaler Raum wird in der Regel mit Vektoren beschrieben.
Vektoren benutzt man überall dort, wo es um die Darstellung geometrischer Figuren
geht. Der große Vorteil von Vektorgrafiken gegenüber Bitmap-Grafiken ist die
Möglichkeit, die Grafik beliebig zu vergrößern oder zu verkleinern, ohne dass eine
merkliche Verschlechterung bei der Ausgabe erfolgt.
An dieser Stelle soll nun kurz auf die elementaren Grundlagen der Vektoralgebra
eingegangen werden, ohne deren Kenntnis ein tieferes Verständnis der Funktionen von
Vektorgrafiken wohl kaum zu verstehen ist. Der Autor bemüht sich aber, so
wenig Theorie wie möglich darzustellen. Vielmehr beschränkt er sich auf das
absolut nötigste. Der interessierte Leser findet in fast jedem Mathematikbuch
ausführliche Erläuterungen zu Vektoren, Transformationsmatritzen von 2D nach 3D
etc.
Um Vektoren darzustellen, benötigt man zunächst ein Koordinatensystem. Das
geläufigste Koordinatensystem ist das ›kartesische Koordinatensystem‹, dessen Achsen
senkrecht zueinander stehen und sich im willkürlich gesetzten Ursprung O schneiden. Die
beiden Einheitsvektoren, die das Koordinatensystem beschreiben, verlaufen parallel zu
den Achsen und werden ex und ey genannt:
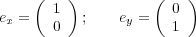 | (10.1) |
Normalerweise wird ein kartesisches Koordinatensystem so gezeichnet, dass die 1.
Achse (x-Achse) von links nach rechts verläuft und größere Werte weiter rechts
angeordnet sind. Die 2. Achse verläuft senkrecht dazu von unten nach oben, wobei
größere Werte weiter oben angeordnet werden. Im Gegensatz dazu werden auf dem
Bildschirm bei der y-Achse größere Werte weiter unten angeordnet. Das heißt, der
Ursprung O liegt in der linken oberen Bildschirmecke. Insbesondere hat ein Bildschirm
nie negative Koordinaten.
Des Weiteren wird kurz auf die vektorielle Darstellung von Punkt, Linie und Kreis in
einem kartesischen Koordinatensystem eingegangen. Ein Punkt lässt sich ganz einfach
durch die Angabe einer x- und y-Koordinate angeben:
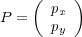 | (10.2) |
Zu unterscheiden ist zwischen dem Punkt P und dem Vektor p, der von O zu P
führt:
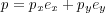 | (10.3) |
|